MVP变换详解

之前学习中对这部分的理解不深，简单补了一遍线代，就又温习了一遍 MVP 变换

概述

MVP 变换简单来说就是将我们已经构建好的各种3维模型映射到屏幕这个2维坐标中， 参与 MVP 变换的信息包括点、矢量、法线、切线等

模型变换（Model）：将模型空间转换到世界空间

观察变换（View）：将世界空间转换到观察空间

投影变换（Projection）：将观察空间转换到裁剪空间

最后要获取屏幕坐标还需要一步：屏幕映射，又叫视口变换

屏幕映射：获取对应屏幕的 2D 坐标

《Shader 入门精要》的配图：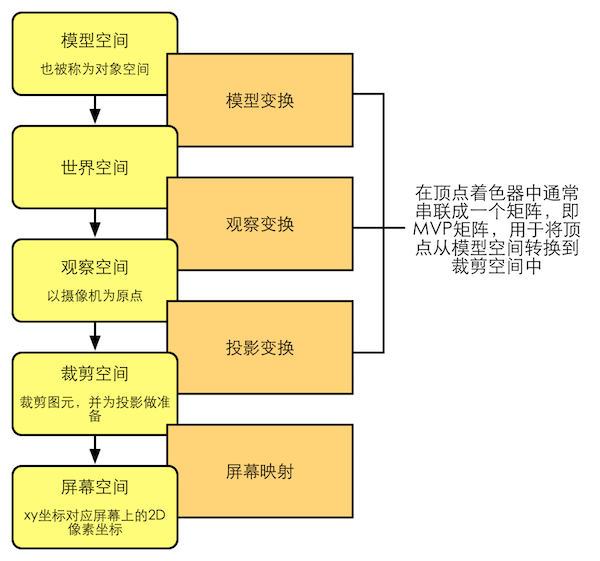

模型变换(Model)

本质就是旋转，平移，缩放（见本文最后）

模型自身会携带模型坐标的原点信息等，再结合世界坐标还是很好变换的

观察变换(View)

在我的理解下，M 和 V 变换本质上是同一种类型的变换

比较快速的方法是把整个摄像机坐标空间移动到世界坐标使二者重合再反转 z 轴（不是真的移动摄像机），即在物体与摄像机相对位置不变的情况下让摄像机位于（0，0，0），将变换摄像机的矩阵作用于物体上就可得到观察空间中的坐标

ps：模型变换也能这么想

投影(Projection)

投影要为裁剪做准备

视野是有限的，所以在视野外（视锥外）的东西是不需要显示的，而用六个裁剪平面（视锥的六个面）直接判断相对复杂，所以需要投影操作将视锥变成裁剪空间，再通过齐次除法，将裁剪空间变成CVV(Canonical View Volume)，OpenGL中CVV就是一个$[-1,1]^3$的正方体（下面讨论这种），DirectX中的 z 分量稍微不同是$[0,1]$，此时的坐标就是 NDC(Normalized Device Coordinates，归一化设备坐标)

不考虑 z 轴的情况下，投影是将所有点投影到近裁剪平面上（个人认为可以理解为摄像机拍到的画面，一张特殊的二维相片），然后放缩到$[-1,1]^2$的正方形平面

而 z 坐标，同样的放缩，但是还需要平移，因为旋向性改变了，z轴变正了（距离越远，z值越大）

所以投影阶段就已经将x,y坐标和z坐标（深度信息）割裂开来了，所谓的 CVV 可能是之前导致我困惑的一点，先分开分析再合并对我来说更好理解一些

正交投影

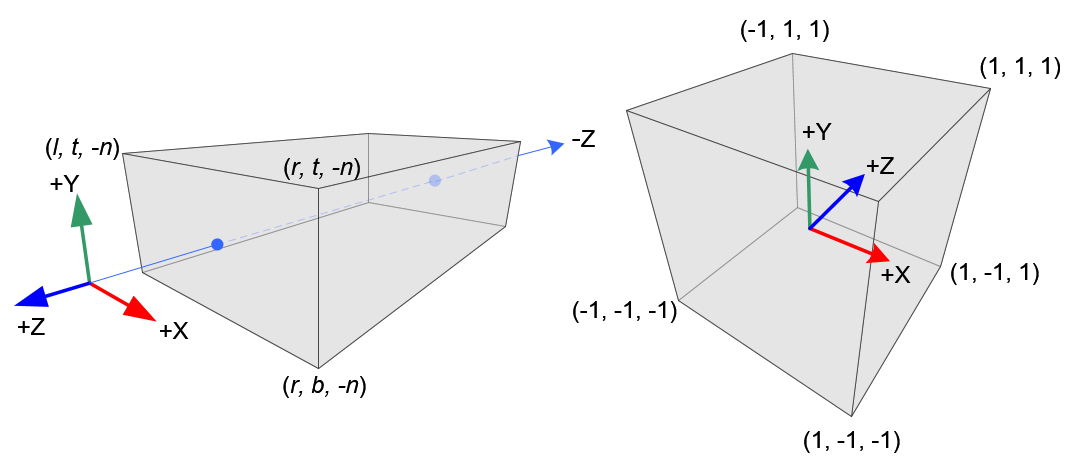
如上图，正交投影的“视锥”是一个长方体，可以通过六个参数定义 right,left,top,bottom,near,far分别对应了x,y,z轴上的范围（n和f是距离），从而构成一个长方体

正交投影的裁剪空间和齐次除法后的CVV是同一个东西就混着讲了

正交投影的XoY坐标不需要变化直接投射到近平面，然后缩放至$[-1,1]^2$
$$
M_{ortho}结构
\left[
\begin{matrix}
a&0&0&0\
0&b&0&0\
0&0&c&d\
0&0&0&1
\end{matrix}
\right]
$$
x,y是简单的放缩
$$
a·x=\frac{x}{\frac{r-l}{2}}
$$

$$
a=\frac{2}{r-l}
$$
y同理

$$
z考虑z_0=-n,z_{normalized}=-1
$$

$$
z_0=-f,z_{normalized}=1
$$

$$
\left{
\begin{aligned}
(-n)c+d=-1\
(-f)c+d=1
\end{aligned}
\right.
$$

$$
解得c=-\frac{2}{f-n}
$$

$$
d=-\frac{f+n}{f-n}
$$

$$
M_{ortho}=\left[\begin{matrix}\frac{2}{r-l}&0&0&0\\0&\frac{2}{t-b}&0&0\\0&0&-\frac{2}{f-n}&-\frac{f+n}{f-n}\\0&0&0&1 \end{matrix}\right]
$$

透视投影

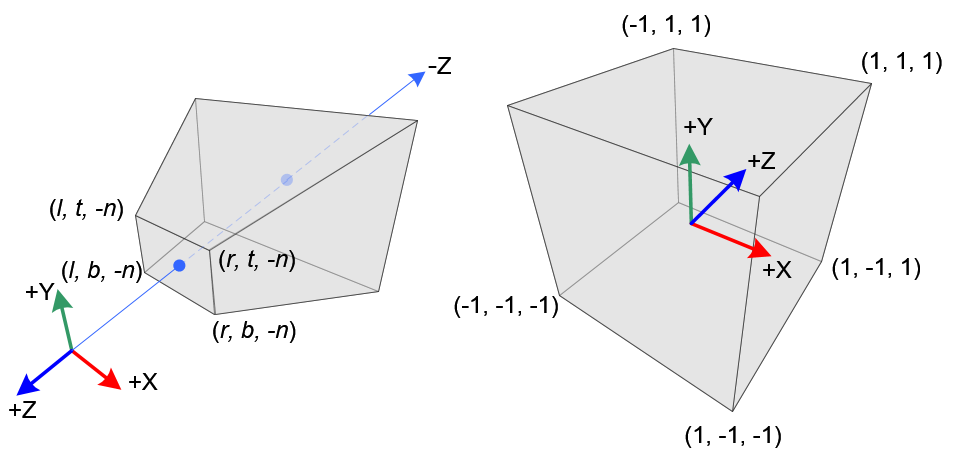
相对于正交投影，透视投影只是多了一条规则：近大远小，即 z 坐标越靠近近裁剪平面投影过来的 x,y 坐标受到的压缩更小

透视投影的视锥由4个参数定义，near,far,FOV,Aspect（FOV 有 FOVx 和 FOVy 之分，Aspect是宽高比 w:h）

对于 XOZ 和 YOZ 平面来说，如下图

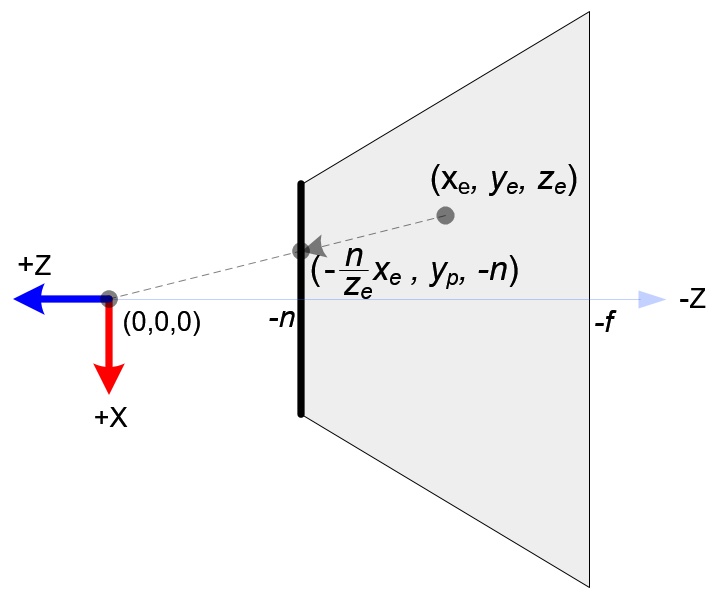
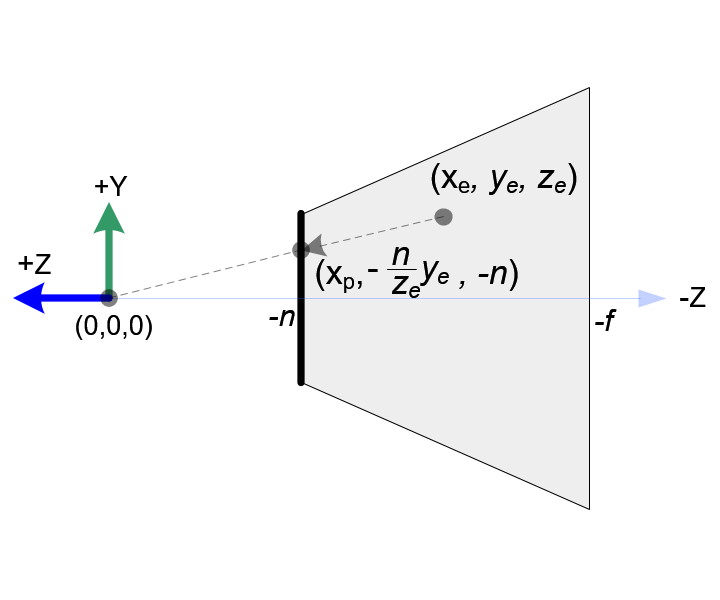
从上图可知，对于 xy 坐标只需要放缩，同时 z 坐标全变为 -n，与xy也没有关系

所以矩阵结构大致如下
$$
M_{persp}=\left[\begin{matrix}a&0&0&0\0&b&0&0\0&0&c&d\e&h&g&i\ \end{matrix}\right]
$$
投影完我们需要将把xy坐标压缩到$[-1,1]^2$范围内
$$
M_{persp}(x_e,y_e,z_e,1)=(x’,y’,z_e’,1)
$$

$$
近平面width=2·near·tan\frac{FOV_x}{2}
$$

$$
近平面height=\frac{weight}{Aspect}=2·near·tan\frac{FOV_x}{2}·\frac{1}{Aspect}
$$
变换后的坐标
$$
x’=\frac{-nx_e}{z_e·n·tan\frac{FOV_x}{2}}=-\frac{x_e}{z_e·tan\frac{FOV_x}{2}}
$$

$$
同理y’=-\frac{y_e·Aspect}{z_e·tan\frac{FOV_x}{2}}
$$
但是由于 xy 的变换涉及到 $z_e$ 很难构建矩阵，所以利用齐次坐标赋予第4个变量其他意义

用数学表示就是让结果同时乘$-z_e$

$-z_e(x’,y’,z’,1)=(-z_ex’,-z_ey’,-z_ez’,-z_e)$

明显可得
$$
a=\frac{1}{\tan\frac{FOV_x}{2}}=\cot\frac{FOV_x}{2}
$$

$$
b=\frac{Aspect}{\tan\frac{FOV_x}{2}}=Aspect·\cot\frac{FOV_x}{2}
$$

$$
e=0 , h=0 , i=0 , g=-1
$$
z轴的矩阵参数分析方法和正交一样
$$
\left{
\begin{aligned}
z_e=-n,z’=-1,-z_ez’=z_e=-n\
z_e=-f,z’=1,-z_ez’=-z_e=f
\end{aligned}
\right.
$$

$$
\left{
\begin{aligned}
(-n)c+d=-n\
(-f)c+d=f
\end{aligned}
\right.
$$

$$
解得
\left{
\begin{aligned}
c=-\frac{f+n}{f-n}\
d=-\frac{2nf}{f-n}
\end{aligned}
\right.
$$

---

$$
M_{persp}=\left[\begin{matrix}\cot\frac{FOV_x}{2}&0&0&0\0&Aspect·\cot\frac{FOV_x}{2}&0&0\0&0&-\frac{f+n}{f-n}&-\frac{2nf}{f-n}\0&0&-1&0\end{matrix}\right]
$$

$$
M_{persp}=\left[\begin{matrix}\frac{\cot\frac{FOV_y}{2}}{Aspect}&0&0&0\0&\cot\frac{FOV_y}{2}&0&0\0&0&-\frac{f+n}{f-n}&-\frac{2nf}{f-n}\0&0&-1&0\end{matrix}\right]
$$
负号有无看f-n还是n-f，再强调一遍 n 和 f 是距离

从推导中可以看出，透视投影后的空间仍然是在一个锥体中(每个图元各自乘自己的 z 坐标)，这个空间是裁剪空间，所以可以认为先推导出 CVV 的公式再获得裁剪空间的变换矩阵
$$
裁剪空间的图元满足以下不等式，就保留
$$

$$
-z_e\leq x\leq z_e
$$

$$
-z_e\leq y\leq z_e
$$

$$
-z_e\leq z\leq z_e
$$

屏幕映射

这一步就要获取图元在屏幕上对应的像素坐标了

正交投影直接获得了 CVV（准确来说是裁剪空间和CVV一样，齐次除法后空间不变），而透视投影需要通过齐次除法（透视除法）来获得 CVV

明白透视投影矩阵的推导过程就很容易理解，透视投影的裁剪空间和 CVV 就差了一个乘除操作$-z_e$，而裁剪空间图元的第四个数就是$-z_e$，所以把裁剪空间图元的 xyz 除以第 4 个数就可获得其在 CVV 中的坐标了

---

获得 CVV 后，z 坐标只用来判断深度大小，关注xy就行
$$
获取屏幕坐标矩阵=\left[\begin{matrix}\frac{width}{2}&0&0&\frac{width}{2}\0&\frac{height}{2}&0&\frac{height}{2}\0&0&1&0\0&0&0&1\end{matrix}\right]
$$

旋转，平移，缩放

这部分的数学推导相对简单就不再赘述

左上 $3*3$ 的矩阵用于旋转和缩放，最后一列用于平移

平移

由于平移不是线性变换，所以采用齐次坐标（齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示，是指一个用于投影几何里的坐标系统）
$$
点的移动\left[\begin{matrix}1&0&0&t_x\0&1&0&t_y\0&0&1&t_z\0&0&0&1\ \end{matrix}\right] · \left[\begin{matrix}x \y\z\1 \end{matrix}\right]=\left[\begin{matrix}x+t_x\y+t_y\z+t_z\1\ \end{matrix}\right]
$$

$$
矢量移动\left[\begin{matrix}1&0&0&t_x\0&1&0&t_y\0&0&1&t_z\0&0&0&1\ \end{matrix}\right] · \left[\begin{matrix}x \y\z\0 \end{matrix}\right]=\left[\begin{matrix}x\y\z\0\ \end{matrix}\right]
$$

旋转

$$
绕 x 轴： \left[\begin{matrix}1&0&0&0\0&cosθ&-sinθ&0\0&sinθ&cosθ&0\0&0&0&1\ \end{matrix}\right]
$$

$$
绕 y 轴：\left[\begin{matrix}cosθ&0&sinθ&0\0&1&0&0\-sinθ&0&cosθ&0\0&0&0&1\ \end{matrix}\right]
$$

$$
绕 z 轴：\left[\begin{matrix}cosθ&-sinθ&0&0\sinθ&cosθ&0&0\0&0&1&0\0&0&0&1\ \end{matrix}\right]
$$

缩放

$$
\left[\begin{matrix}k_x&0&0&0\0&k_y&0&0\0&0&k_z&0\0&0&0&1\ \end{matrix}\right]
$$

$k_x=k_y=k_z$时为统一缩放