Gamma校正详解
Gamma校正详解
首先,物理上灰度的变化是平滑的,两倍的光子就产生两倍的灰度变化,是线性的,但是在人眼中就不同了,人眼对暗部更加敏感,是非线性的
打个比方就是在暗处 0.5 倍的物理光子变化,在人眼中可能变化了 2-3 倍,而在亮处,要让人感到 2 倍的亮度变化,光子可能需要增加 3-4 倍

如上图,线性空间(物理空间)中的 0.2 在人看来就是美术意义上的中灰
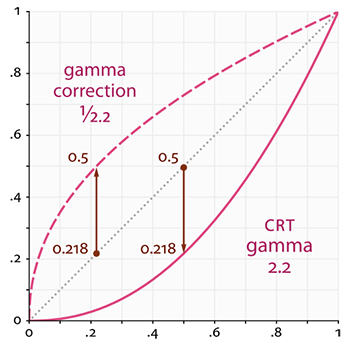
简易的一个例子
假设自然界中一个 0.218 的灰度,在人眼中就是 0.5
用相机等光学元件记录时,记录的就是 0.218(大多数数码相机以线性方式记录光线)
经过 gamma 校正(gamma 编码),0.218 通过传递函数以 0.5 存储在硬盘中(这一步在现实中,由绘图软件本身做了,存储在 jpg 等格式的文件中)
显示时经 gamma2.2 压暗,以 0.218 的光显示,人眼中就是 0.5,和最开始直接观察一致
- 如果不校正直接存储在硬盘中,经过 gamma2.2 的压暗输出 0.035,人眼中就是 0.218,结果我们直接看到了线性空间,就是图一的第二行,导致图片的视觉效果非常亮,而且在人眼中的黑到灰被压缩到了 0.0-0.2,图片的暗部没有细节,而且从黑到白的过度非常生硬有跳跃感,下面是在 unity 中做的效果
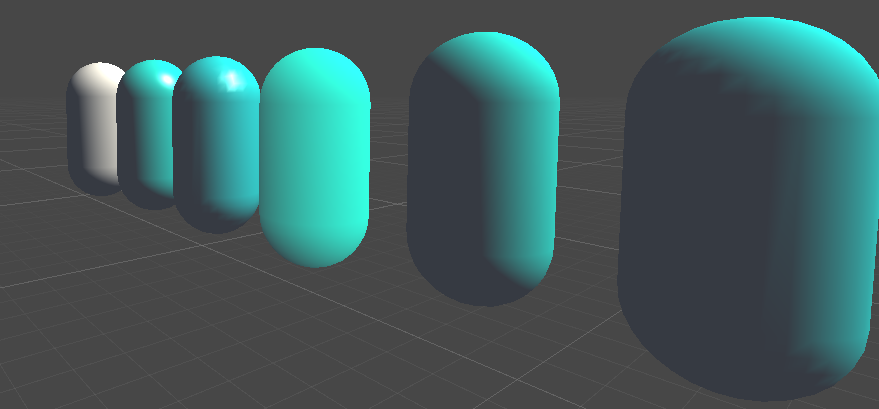
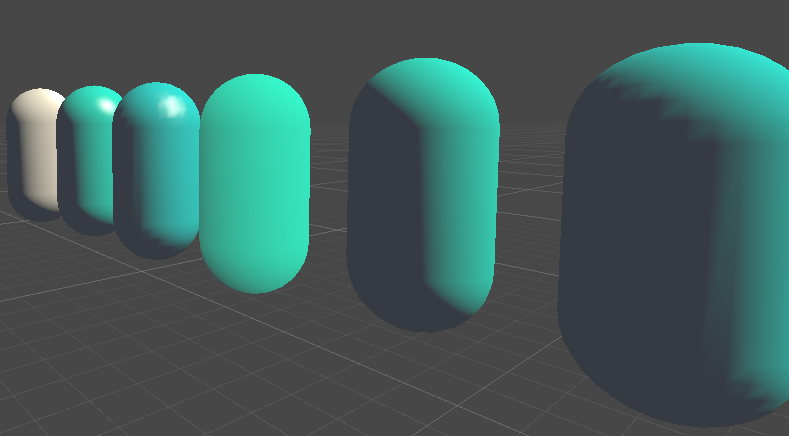
左图Gamma校正,右图无Gamma校正,灰色过度几乎没了,由于只是简单的光照模型没用贴图,所以不能直观感受暗部的细节缺失
sRGB 贴图过曝问题
sRGB空间 在内存中就是 1/2.2的伽马编码,非线性的编码
当我们在渲染器中使用gamma校正后,就是对原图又进行了一次亮度提升,特别明显的是超出 1.0 的部分被截断在 1 导致大量的纯白
另一个就是混合操作时,直接拿非线性编码混合就出问题了,需要转换到线性空间下再参与计算
1 | float gamma = 2.2; |
并非所有纹理实际上都在 sRGB 空间中。用于为对象着色的纹理(如漫反射纹理)几乎总是在 sRGB 空间中。用于检索光照参数的纹理(如镜面反射贴图和法线贴图)几乎总是在线性空间中
光照衰减
由于 gamma 校正的影响
一句话总结:线性空间用线性,伽马空间用物理方程
线性空间中用经验方程
$$
线性空间中的变化\frac{1}{D}
$$
$$
经过显示gamma后,显示亮度为\left(\frac{1}{D}\right)^{2.2}=\frac{1}{D^{2.2}},差不多2次幂
$$
unity对sRGB图像的处理
贴图选项勾选 sRGB 在采样时就将伽马空间中的数值转到线性空间中了(重校),经过着色器操作,最后输出到屏幕之前通过 sRGB Frame Buffer 进行 gamma 校正以平衡显示器的显示gamma







